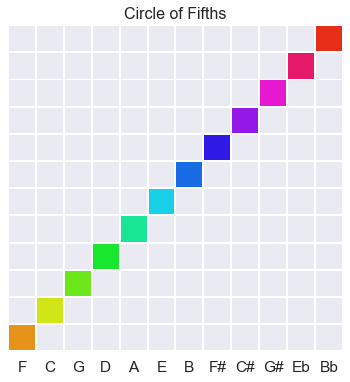
Up to now, I’ve been showing these bit-groups in black and white, like a piano. But doesn’t do justice to the differences within the 12-bit bandwidth. An octave makes a sort of spectrum. To begin, here is the circle fifths, visible and audible.
This serves as a kind of identity matrix, serving specifically to mark the presence or absence of powers of three.
The Circle of Fifths as Groups of Seven Notes
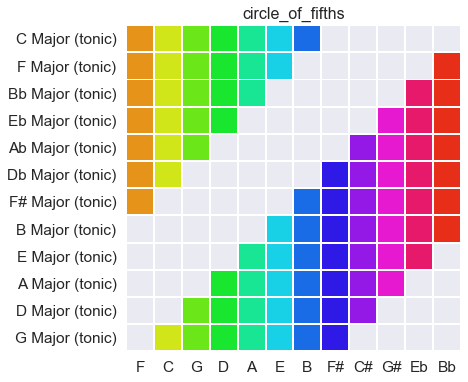
Each row in the graph below contains the notes of a key, represented by seven bits. Modulation, in this system, is possible with a circular bit-shift. However, keys are large categories: when you hear the scales next to each other, they are a bit hard to distinguish, though I suppose it’s clear there’s a kind of downward spiral.
But what’s more important is what each key is capable of containing, and how it defines not only what notes to play, but what notes one might predict even without having heard them.
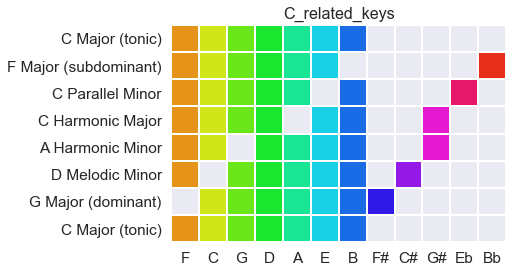
Sets of Related Keys
Each major key, in this system and in conventional harmony, has a set of related keys. Here they are defined moving one bit seven places to the left (flat-side: subdominant, parallel minor) or right (sharp-side: dominant, melodic minor, relative harmonic minor).
Interestingly, moving one bit seven places the same amount of ‘work’ as moving seven bits one place each, as in the circle of fifths, above.
Perhaps still more interestingly, this group of scales allows all twelve notes to be used within a single key area, as often happens in musical reality.
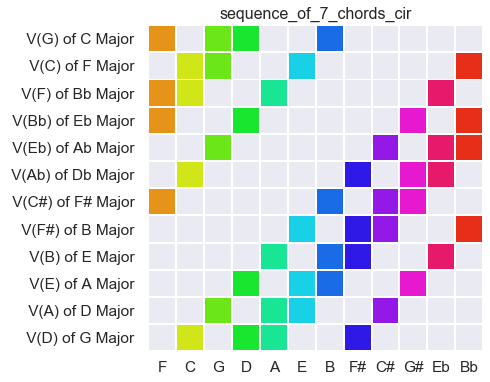
Dominant Sequence around the Circle of Fifths
Here is a sequence of dominant 7th chords. Each gives the full outline of a key, but is entropic enough to be heard either as a series of individual notes or as a sequence of chords
Dominant Sequence around the Related Keys
Here’s a similar sequence to the previous one, but with a shortcut. It finds its way home in 7 steps rather than twelve, without ever losing tonal orientation. (The evenly-spaced diminished chord in the fourth row allows the slip. ‘Harmonic Major’ is a bit tricky to hear, but it plays a role here, as it does in Cole Porter’s Night and Day.)
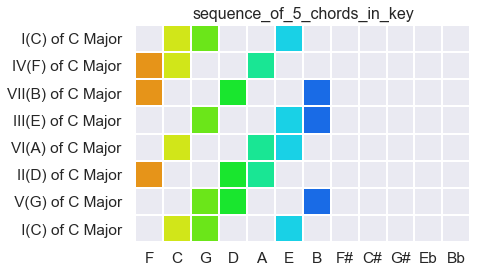
Sequence of chords within one key
And here is what happens when you stay in one key: the bandwidth narrows. The prediction space finds solid footing, and orientation is clear.
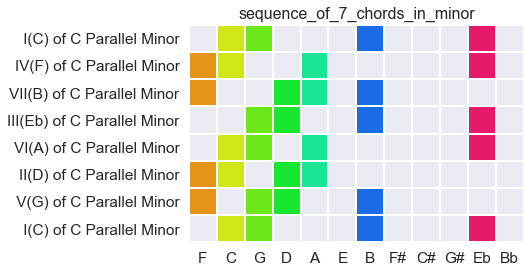
Sequence of chords within a minor key
A minor key, if it exists on its own, is a major key with a bit-wrinkle in it. Here, for example, the essential bandwidth of C Major remains (the range from F to B), but E becomes Eb, creating an audible change of balance.
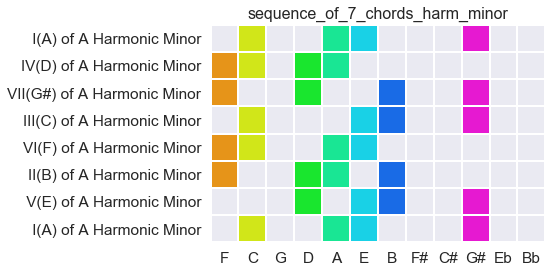
Harmonic minor is similar. it replaces G with G#. But a curious thing happens: the G# re-orients the C Major bandwidth around A. It is almost as though one hears a new 7-tone bandwidth, running from D to G#:
So that’s a quick tour. Patterns emerge. These patterns don’t make music in themselves, but they do make some the ingredients out of which music can be made.
Advantages
- Each key is identifiable as a distinct 7-bit bandwidth in a 12-bit space.
- Related keys are definable using only simple logic operations. Minor keys are defined by the increased entropy in their organization.
- Because it is a bit-combination, each scale is a maximally efficient logical filter, measuring inclusion of a frequency in a key area. Categorization of musical sounds within harmony can thus occur with almost no computational overhead.
- Categorization of keys brings a distinct, intrinsic musical identity aligned with many existing traditions of notation – not to mention a bar-code identity.
- A prime numbered set of pitches allows for unique algorithmic generation of patterns-within-patterns. This will prove useful for building chords and categorizing chords, as we will see in the next post.
- A small backpropagation (with earth-moving distance serving as its naive loss function) can calculate the probable context of anay given group of identified notes in either an audio or notation context. That will be for… two posts later.