scale- and chord-building | Timothy Summers

One advantage of this ternary system is that a lot of the crazy folds and skips of scales and arpeggios – even in quite advanced tonalities – turn out to be pretty simply algorithmic.

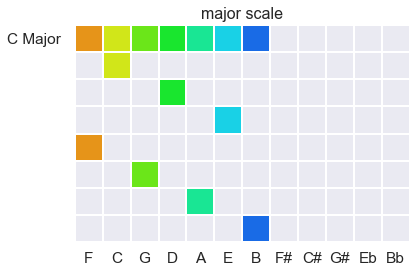
Here, for example, is what you get when you take every second bit in the F-to-B group of bits, starting on C. You will here the whole scale as a series, then each individually, as pictured:

As you can see, and hear, every half-step in the scale comes from the space folding back on itself.

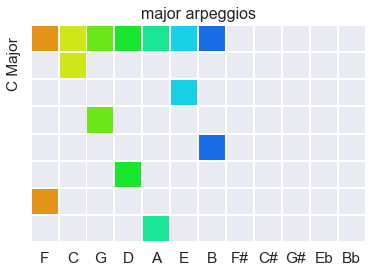
Similarly, here is what you get when you skip to every fourth bit. It will also sound familiar:

Just as in the scale, every minor interval in the arpeggio is generated by the space folding back on itself.

This seems like a lot of information for just a few bits, but it works because the information is in the system of the bits themselves.

building scales: a closer look

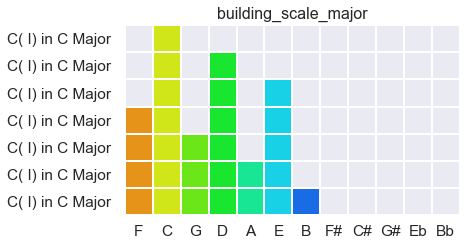
Each regular stride across the space will bring a very familiar musical structure. These combinations of individual notes begin to indicate modal areas. Chords and scales serve as intermediaries between the singleness of notes and the multiplicity of keys.

Here, for example, is a scale forming in major (the reverse of what is pictured above):

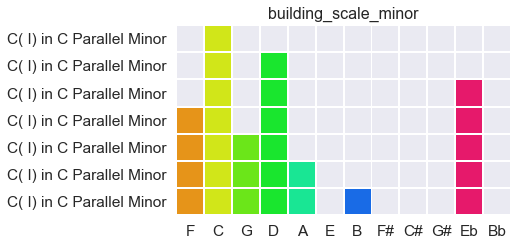
And here is a scale forming, similarly, in minor. Remember that the Eb is effectively taking the place of E, so the same ‘staircase’ pattern is in effect:

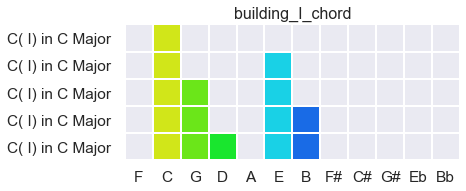
building chords: stable simultaneity

Thirds are far enough from one another in frequency not seem like conflicting versions of the same note. So simultaneity of two voices (polyphony) becomes unmistakeable with piles of thirds.

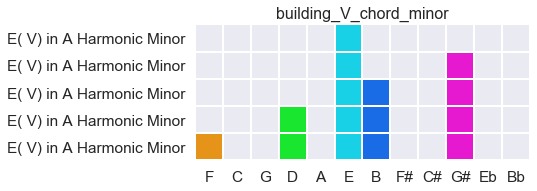
Furthermore, this system of building chords works very nicely in minor. Here, for example, is V in A Harmonic minor, which nicely takes into account the flat 2:

modes as patterns within the patterns:

Of course, there’s a great deal going within each key. Modes, which start on different notes of a single scale pattern, are not differentiable from each other when taken as a sets (as you can see below). There is, however, an audible importance to the beginning of a pattern. These, too, are algorithmically definable.

Although it may not be directly evident from a first hearing, all of the scales in the audio above have exactly the same notes (adjusted for register). They do have different functions and balances, though, dependent solely upon which note they start with. These are the modes, and they are real enough to hear, even when they may in some ways look indistinguishable from one another.

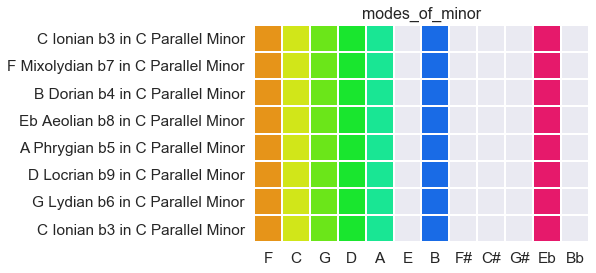
modes in minor

Naturally, the same applies for modes of minor scales. Don’t let the fancy names at the left in the bottom throw you: it’s exactly the same pattern as in major. The Eb at the far right just folds into the former place of E, and the same algorithm applies: if you play the note in every second column, you will hear a scale. Different starting points yield different modes.

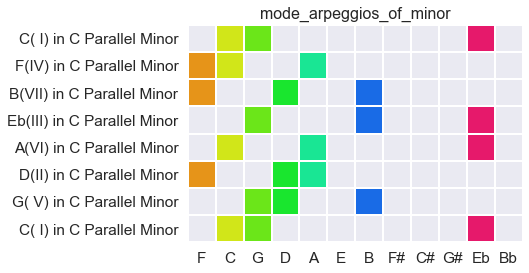
arpeggios: non-simultaneous chords

The impression of a key is just as strong with 3-note arpeggios as it is with entire scales. Arpeggios bring tremendous flexibility. They are sets of notes which imply larger sets of notes, and allow our ears to predict some sort of completeness beyond them. Ornament becomes possible; small surprises can appear in the gaps; a great deal ends up being ‘heard’ without ever being audible.

Here are some arpeggiated examples in both harmonic and melodic minor:

on the algorithmic generation of these models

Every one of the sequences above (and infinite others) can be generated using the absolute minimum of particular and wave representation. The sounds are sine waves based on frequencies; the images are twelve bits per row.

These harmonic sequences show a surprising amount of intrinsic information, given their small resources. The tensions inside these chords are non-trivial generative sources for musicians and listeners.

I won’t vouch for the musical value of these systems in and of themselves, but they do reflect patterns that appear commonly in both notated and improvised music – and not only in so-called Western music.

Lastly, it is worth mentioning the total information necessary to generate the information in each of the graph/sound pairs above, is something like this:

This makes a total of 32 bytes for some fairly complex information. (This sentence is 32 bytes long.) Your average jazz standard would have an information germ of about 80 bytes, give or take, in this format.

Moreover, these numbers not only identify bit combinations in a taxonomic or indexed way, like barcodes; they define a (probable) function and direction in musical time and space. They open up possibilities for memory and for extrapolation. This kind of encoding is, to put it briefly, open for interpretation, and prepared to take off in many directions.