The rolling-down-a-hill of backpropagation with gradient descent has proven enormously powerful. The process of identifying chords in a ternary harmony system is curiously similar, though the loss function is far more naïve and transparent. Instead of using derivatives, the algorithm simply derives the smallest earth-moving distance, at bit level. It’s rather prosaic.
But what this musical/computational process lacks in sophistication it makes up for in mechanical efficiency, and its musical yield is more than trivial. In the end, this system for categorization of chords will look like the network below, with input left and output right:
To reach this model, though, we will have to think a bit about the function of notes and chords. It is a musical topic which is easy to feel, but hard to describe. So we will advance step by step. The network/node model will prove useful in future posts. It does have a kind of neural-net look to it, and that may or may not be relevant.
notes alone
To begin with: a note alone can mean just about anything. A note tells that there has been an event whose resulting sound frequency is consistent and thus identifiable.
If we consider a single note in the twelve-note world of ternary harmony, it may seem to have any one of 49 possible functions. Below is an map of these possible harmonic roles (C is yellow: each horizontal strip represents a potential key and function) along with an audio rendering of all of those keys. There are more than might be usefully listed or meaningfully considered by ear:
This is not a practical list, at least not from a human standpoint. It is worth pointing out, though, that since only a single logic operation (&) is required to parse these possibilities, it’s pretty efficient even in the worst case.
note groups (chords)
Groups of notes tell us much more than single notes, and not only because they come in quantity. They radically limit the possibilities for definition of context (much as a few data points can indicate a whole demographic and set of behaviors). Chords, when they consist of notes separated enough not to directly interfere with each other, allow their components to remain aurally distinct. Listeners can understand them as a set of distinct identities working together. Chords are singular and plural.
Below you can see how the potential harmonic function of a chord is far more narrowly defined than that of a single note (shown in the graph above). It still gives a fair number of possibilities to consider, but it clearly provides a more focused set of possibilities. The C major triad below has 18 possible functions. (Some of which are duplicates in related keys, e.g. C Major is a tonic key, but can also serve as a temporary dominant key related to F Major. But this matters only in long-term memory, which we will come to later).
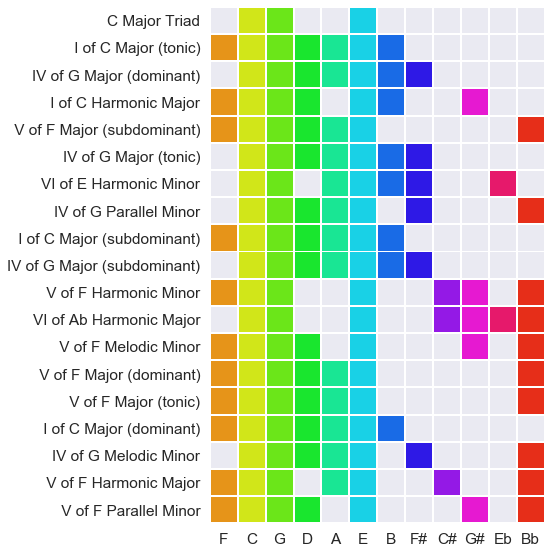
A ‘seven’ chord, which uses four notes, limits the potential keys still further, to 8 (three of which are duplicates, as above). This gives a quite stable sense of tonality:
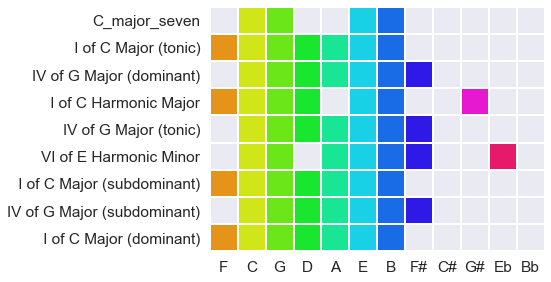
Chords alone can imply many functions, consequences, and tensions of the notes they contain, with surprising specificity.
But although chords do supply critical context for notes, they also can imply a deeper context. The context which chords require comes from remembering the past and predicting the future.
This brings us to the idea of key.
key as a hidden state
A key provides orientation for memory and prediction, but it is not directly heard at any given moment. It is only real insofar as it allows prediction and exists in memory. You might say that the idea of a key constitutes a ‘hidden state‘, whose contents and meaning show up in practise and over time. Musically, this makes sense: we require not only sounds, but a field for anticipation, prediction, tension and release. Single tones are literally monotonous, and clusters of tones are figuratively monotonous. But a sense of direction and possibility is a real part of musical reality – we find these qualities between the idea of a note and the idea of a key.
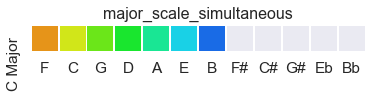
Keys do not make sense when you hear their contents all at once. Here, for example, is C Major as a cluster. It’s not outright cacophonous, but does tend toward being a sound-cloud:
The pentatonic scale (aka 6/9 chord) seems to live right at the limit of what we can discern in simultaneous sounds:
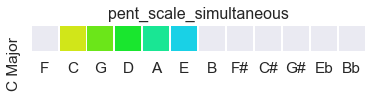
What is crucial to know is that these keys – prime-numbered in their parts and distinct from one another – exist in memory and prediction. We experience them over time. They are not physical sounds.
naïve backpropagation: finding the root and degree of a chord
Given a group of notes, though, how do we find which note is the most important? It turns out that if we assume a seven-note or five note scale (which of course includes smaller scales), we can find the root of a chord in a few steps, but reaching back into the hidden states.
For each of the possible keys in which a chord might live (shown in the long lists above), we can test how efficiently the group of notes can exist within it.
Let us take the example of a C major triad (as usual). Given three notes, one of them must be the ‘root’. So let us try building in thirds from G, using the key of C major:
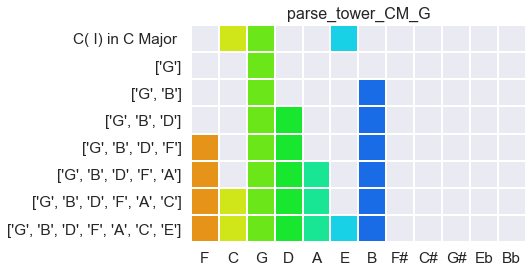
You can see that it takes six steps to find C again. Not very good. Next, try building in thirds from E:
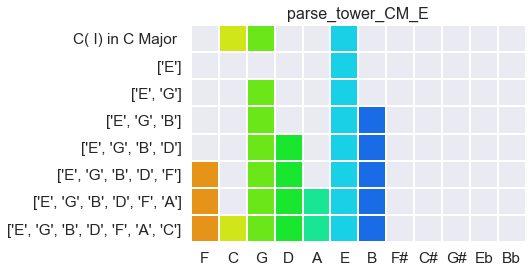
Just as bad: six moves away. And starting from C?:
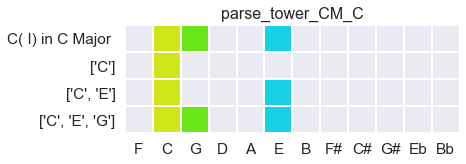
Three steps. Lovely. The most efficient algorithm yields the perceived root – and this discovery can be cleanly implemented using binary logic operations.
Additionally, this backprop-lite technique is quite flexible, allowing for the understanding partial voicings. Here, for example, is the process of finding the root of a dominant 7 chord without a 5, on A-flat:
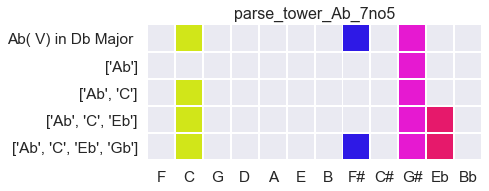
Add a flat 9 and it still gets found:
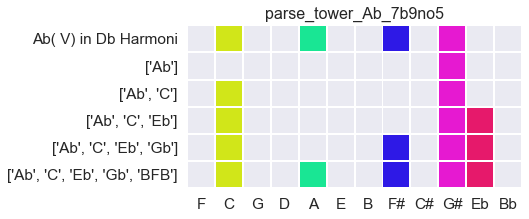
This turns out to be a process which operates with considerable precision even at the speed of audio analysis.
key as a prediction area
Once you know all the functions that a chord might serve, and what note serves as it root, you can investigate which function it does serve.
Unfortunately, there is no way of really knowing this (even within the assumption that musical tensions exist). And even inside this ternary system, there are several kinds of possible surprise, the clearest of which is that the chord serves as a hinge, fulfilling one purpose toward the past, and another the future. A chord can clearly exist in two keys at once — one for the past, and one for the future.
But assuming a key allows us to hear and predict does have some reality to it. Keys allow us to encounter many combinations of notes without making any significant alteration to underlying expectations. For example: if we hear a C Major chord, and we hear a G Major chord, we figure the two of them can come together to define a single undifferentiated bandwidth called the Key of C Major:
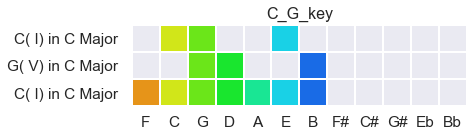
A ii-V-I progression is even more complete, with no note of C Major left unheard:
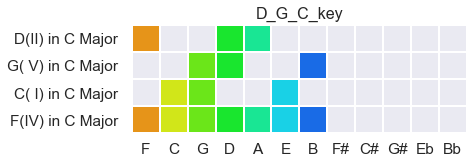
Last, you can begin to see (and systematically measure) not only how keys fit within a tonality, but how a prediction space can bend without breaking, through the addition strategic single notes:
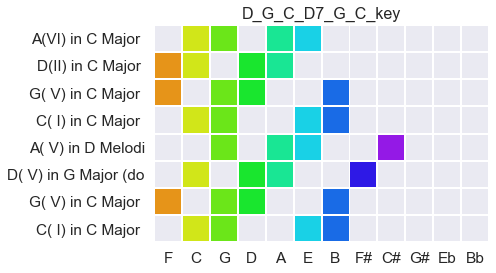
So what we hear at any moment fits into some larger pattern over time. The question becomes not only ‘how far is one chord from another?’, but ‘how far is one prediction space from another?’.
And in this way, we may be able to measure some parameters of tension, release, memory, and prediction in harmony.